浅谈Quicksort（快速排序）

题外话

最近在修炼内功的同时，也试图把一些常见的高频算法捡起来上手操作一下，温故而知新总是有道理的，期间查阅了各种渠道的资料来辅助记忆，但是发现到手的大部分资料都或多或少有些「照本宣科」的成分，加上「快速排序」这个知识点存在多种实现思想，看过一些视频后反而觉得大脑混沌杂乱，也感慨道有些粉丝量不少的博主在视频中讲解知识点时也会有层次不分明和不尽人意的地方，或许独立学会某个知识点和教会他人一个知识点这两件事之间并不是某种意义上的等价，遂打算爬帖来阅读，也终于在腾讯云社区找到一篇干货帖子，逻辑清晰并且可靠，帖子标题为【算法图文动画详解系列】QuickSort 快速排序算法，这期内容主要援引自这篇帖子，打算作为「快速排序」问题的标准答案记录下！

1.快速排序简介

快速排序（Quicksort）是对冒泡排序算法的一种改进。

快速排序由C. A. R. Hoare在1960年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

2.快速排序原理

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

1. 首先设定一个分界值（pivot）：通过该分界值将数组分成左右两部分（partition）
2. Compare and Swap（比较&交换）：将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。
3. Recursive（递归）：然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4. 重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

• 综上总结核心思想：分治 + 取分界点 + 递归

3.详解快速排序

快速排序（QuickSort ）是一个分治算法（Divide and Conquer）。它选择一个元素作为枢轴元素（pivot），并围绕选定的主元素对给定数组进行分区（partition）。

快速排序有很多不同的版本，它们以不同的方式选择枢轴：

1. 总是选择第一个元素作为 pivot。
2. 总是选择最后一个元素作为 pivot。
3. 随机选一个元素作为 pivot。
4. 选择中值作为 pivot。

QuickSort 中的关键步骤是 partition()。在数组中选择的一个元素为支点（pivot）, 把所有小于 pivot 的元素放到 pivot 左面, 大于 pivot 的放右边。这样数组 x[n] 会被划分成3个部分：

Part 1：x[0] , ... , x[pivot - 1]

Part 2：x[pivot]

Part 3：x[pivot+1] , ... , x[n]

所有这应该是在线性时间内完成。

接下来，就是递归调用:

 quicksort(x, low, pivot - 1)
 quicksort(x, pivot + 1， high)

下面附上快速排序伪代码逻辑：

/* low  --> Starting index,  high  --> Ending index */
void quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

下面附上求分界点位置伪代码逻辑：

/* This function takes last element as pivot, places
   the pivot element at its correct position in sorted
    array, and places all smaller (smaller than pivot)
   to left of pivot and all greater elements to right
   of pivot */
partition (arr[], low, high)
{
    // pivot (Element to be placed at right position)
    pivot = arr[high];  
 
    i = (low - 1)  // Index of smaller element and indicates the 
                   // right position of pivot found so far

    for (j = low; j <= high- 1; j++)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++;    // increment index of smaller element
            swap arr[i] and arr[j]
        }
    }
    swap arr[i + 1] and arr[high])
    return (i + 1)
}

下面附上排序逻辑实现过程：

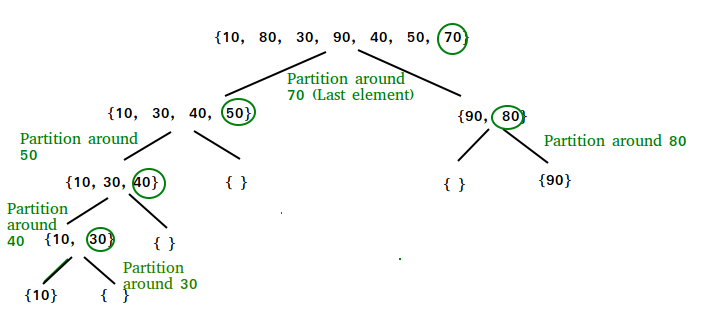
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes:  0   1   2   3   4   5   6 

low = 0, high =  6, pivot = arr[h] = 70
Initialize index of smaller element, i = -1

Traverse elements from j = low to high-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0 
arr[] = {10, 80, 30, 90, 40, 50, 70} // No change as i and j 
                                     // are same

j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]

j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // We swap 80 and 30 

j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]

j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 and 40 Swapped
j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j] 
i = 3 
arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 and 50 Swapped 

We come out of loop because j is now equal to high-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[high] (or pivot) 
arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 and 70 Swapped 

Now 70 is at its correct place. All elements smaller than
70 are before it and all elements greater than 70 are after
it.

附：快速排序Java实现代码

下面贴上使用Java实现的快速排序代码：

// Java implementation of QuickSort
import java.io.*;

class QuickSort{
    
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
static int partition(int[] arr, int low, int high)
{ 
    // pivot
    int pivot = arr[high];
    
    // Index of smaller element and
    // indicates the right position
    // of pivot found so far
    int i = (low - 1);

    for(int j = low; j <= high - 1; j++)
    {
        // If current element is smaller
        // than the pivot
        if (arr[j] < pivot)
        {
            
            // Increment index of
            // smaller element
            i++;
            swap(arr, i, j);
        }
    }
    swap(arr, i + 1, high);
    return (i + 1);
}

/* The main function that implements QuickSort
        arr[] --> Array to be sorted,
        low --> Starting index,
        high --> Ending index
*/
static void quickSort(int[] arr, int low, int high)
{
    if (low < high)
    {
        // pi is partitioning index, arr[p]
        // is now at right place
        int pi = partition(arr, low, high);

        // Separately sort elements before
        // partition and after partition
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

public static void main(String[] args)
{
    int[] arr = { 10, 7, 8, 9, 1, 5 };
    int n = arr.length;
    
    quickSort(arr, 0, n - 1);
}
}

// This code is contributed by Ayush Choudhary

优美的代码值得被记录，原帖内容精炼且满满都是干货，留给我补充的余地不多，所以本期内容摘抄居多，希望能够帮助到你！

By the way：快速排序虽然基础，但依旧耐人寻味